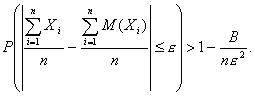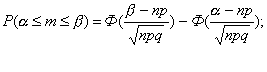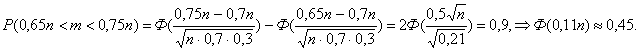ЛЕКЦИЯ 10
ТЕМА: ЗАКОН
БОЛЬШИХ ЧИСЕЛ
1.
Введение.
2.
Неравенство Чебышева.
3.
Теорема Чебышева.
4.
Теорема Бернулли.
5.
Теорема Муавра- Лапласа.

1.
Введение.
При
изучении теории вероятностей приходится
использовать понятия случайного события
и случайной величины. При этом предсказать
заранее результат испытания, в котором
может появиться или не появиться то или
иное событие или какое-либо определенное
значение случайной величины, невозможно,
так как исход испытания зависит от многих
случайных причин, не поддающихся учету.
Однако
при неоднократном повторении испытаний
могут наблюдаться определенные
закономерности. Эти закономерности,
свойственные массовым случайным явлениям,
и изучает теория вероятностей. Следует
отметить, что математические законы
теории вероятностей получены в результате
абстрагирования реальных ситуаций, в
которых наблюдаются случайные массовые
явления.
При
изучении результатов наблюдений над
реальными случайными массовыми явлениями
также имеют место некоторые
закономерности. Следует обратить внимание
на то, что они обладают свойством
устойчивости. Суть этого свойства состоит
в том, что конкретные особенности каждого
отдельного случайного явления почти не
сказываются на среднем результате большой
массы подобных явлений, а характеристики
случайных событий и случайных величин,
наблюдаемых в испытаниях, при
неограниченном увеличении числа
испытаний становятся практически не
случайными.
 Теоремы закона больших чисел
устанавливают зависимость между
случайностью и необходимостью.
Теоремы закона больших чисел
устанавливают зависимость между
случайностью и необходимостью.
Закон
больших чисел- это обобщенное название
нескольких теорем, из которых следует, что
при неограниченном увеличении числа
испытаний средние величины стремятся к
некоторым постоянным.

2.
Неравенство
Чебышева.
 Лемма:
Если случайная величина Х имеет конечные
математическое ожидание М(Х) и дисперсию Д(Х),
то для любого положительного e
справедливо неравенство
Лемма:
Если случайная величина Х имеет конечные
математическое ожидание М(Х) и дисперсию Д(Х),
то для любого положительного e
справедливо неравенство
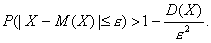
Данное
неравенство часто дает грубую, не
представляющую интереса оценку. Например,
пусть
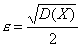 ,
,
тогда
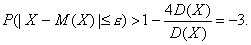
Тем
не менее данное неравенство имеет большое
теоретическое значение. С его помощью
доказываются теоремы и делаются
теоретические выводы.

3.
Теорема
Чебышева.
 Теорема Чебышева: При достаточно
большом числе независимых случайных
величин Х1, Х2, Х3, ..., Хn, дисперсия каждой из
которых не превышает одного и того же
постоянного числа В, для произвольного
сколько угодно малого числа e справедливо
неравенство
Теорема Чебышева: При достаточно
большом числе независимых случайных
величин Х1, Х2, Х3, ..., Хn, дисперсия каждой из
которых не превышает одного и того же
постоянного числа В, для произвольного
сколько угодно малого числа e справедливо
неравенство
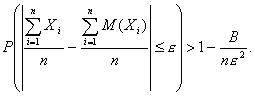
Из
теоремы следует, что среднее арифметическое
случайных величин при возрастании их числа
проявляет свойство устойчивости, т. е.
стремится по вероятности к неслучайной
величине, которой является среднее
арифметическое математических ожиданий
этих величин, т.е. вероятность отклонения по
абсолютной величине среднего
арифметического случайных величин от
среднего арифметического их
математических ожиданий меньше чем на e
при неограниченном
возрастании n стремится к 1,
т.е. становится практически достоверным
событием.
 Рассмотрим
частный случай теоремы Чебышева:
Рассмотрим
частный случай теоремы Чебышева:
Пусть при n испытаниях наблюдаются n
значений случайной величины X,
имеющей математическое ожидание M(X) и
дисперсию D(X). Полученные
значения можно рассматривать как случайные
величины Х1, Х2,
Х3, ..., Хn,.
Это следует понимать так. Серия из п
испытаний проводится неоднократно. Поэтому
в результате i-го испытания, i=l,
2, 3, ..., п, в каждой
серии испытаний появится то или иное
значение случайной величины X,
не известное заранее. Следовательно, i-e
значение xi
случайной величины, полученное в i-м
испытании, изменяется случайным образом,
если переходить от одной серии испытаний к
другой. Таким образом, каждое значение xi можно
считать случайной величиной Xi
.
Предположим,
что испытания удовлетворяют следующим
требованиям:
1) испытания независимы. Это
означает, что результаты Х1,
Х2, Х3, ..., Хn
испытаний—независимые случайные величины;
2) испытания проводятся в
одинаковых условиях—это означает, с точки
зрения теории вероятностей, что каждая из
случайных величин Х1,
Х2, Х3, ..., Хn
имеет такой же закон распределения, что и
исходная величина X,
поэтому, MXi=MX и DXi=DX, i=1,
2, .... п.
Учитывая
вышеуказанные условия, получим
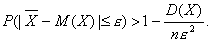
Переходя
к пределу, имеем
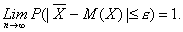
Из
последнего равенства следует, что среднее
арифметическое случайной величины Х
обладает свойством устойчивости.
Теорема
Чебышева имеет большое практическое
применение. Она позволяет, используя
среднее арифметическое, получить
представление о величине математического
ожидания, и наоборот. Так, измеряя
какой-либо параметр с помощью прибора, не
дающего систематической погрешности, можно
получить достаточно большое число
результатов измерений, среднее
арифметическое которых по теореме Чебышева
будет практически мало отличаться от
истинного значения параметра.
Пример.
Пусть в результате 100 независимых испытаний
получены случайные величины Х1, Х2,
…, Х100 с
равными математическими ожиданиями М(Х)= 10 и
равными дисперсиями D(X)= 1.
Оценить вероятность того, что среднее
арифметическое случайных величин
отклоняется по абсолютной величине от М(Х)
меньше чем на 1/2.
Решение:
Имеет
место частный случай теоремы Чебышева.
Применяя соответствующее неравенство для
оценки вероятности, получим:
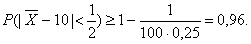

4.
Теорема Бернулли.
 Теорема
Бернулли: Если вероятность события А в
каждом из п независимых испытаний
постоянна и равна р, то при достаточно
большом п для произвольного e >0
справедливо неравенство
Теорема
Бернулли: Если вероятность события А в
каждом из п независимых испытаний
постоянна и равна р, то при достаточно
большом п для произвольного e >0
справедливо неравенство
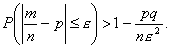
Переходя
к пределу, имеем
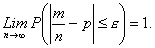
Теорема
Бернулли устанавливает связь между
вероятностью появления события и его
относительной частотой появления и
позволяет при этом предсказать, какой
примерно будет эта частота в п
испытаниях. Из теоремы видно, что отношение т/п
обладает свойством устойчивости при
неограниченном росте числа испытаний.
 Иногда
(при решении практических задач) требуется
оценить вероятность того, что отклонение
числа т появления
события в п
испытаниях от ожидаемого результата пр
не превысит определенного числа e.
Для данной оценки неравенство переписывают
в виде
Иногда
(при решении практических задач) требуется
оценить вероятность того, что отклонение
числа т появления
события в п
испытаниях от ожидаемого результата пр
не превысит определенного числа e.
Для данной оценки неравенство переписывают
в виде
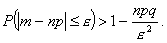
Пример1.
Монету подбрасывают 1000 раз. Оценить
вероятность отклонения частоты появления
герба от вероятности его появления меньше
чем на 0,1.
Решение:
Вероятность
появления герба р= 0,5, тогда q =
1- 0,5= 0,5; n=
1000, e = 0,1. Используем
теорему Бернулли:
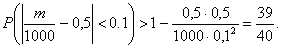
Расшифруем
неравенство
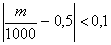
Раскрывая
модуль и решая неравенство относительно
m
получим: 400<m<600. Итак, вероятность
отклонения частоты появления герба от
вероятности его появления равна
вероятности того, что герб выпадет от 400 до
600 раз из 1000 и равна 39/40.
Пример2.
В урне 100 белых и 100 черных шаров. Вынули с
возвращением 50 шаров. Оценить вероятность
того, что белых шаров среди вынутых
окажется более 15 и менее 35.
Решение:
Используем
теорему Бернулли в виде:
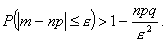
Вероятность
достать белый шар при каждом испытании
равна р=100/200=0,5, тогда q
=0,5. Для вычисления
e
раскроем
модуль и получим
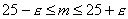
Учитывая
данные задачи, получим систему уравнений,
решая которую найдем e:
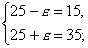
откуда
e =10.
Подставим
значения и оценим вероятность
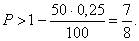

5.
Теорема
Муавра- Лапласа.
Формулировка
теоремы рассмотрена ранее.
 Отметим,
что данная теорема описывает переход от
биноминального распределения к
нормальному при неограниченном росте числа
испытаний n. Теорема позволяет
вычислить вероятность попадания СВ в
интервал и вероятность отклонения по
абсолютной величине случайной величины от
своего математического ожидания:
Отметим,
что данная теорема описывает переход от
биноминального распределения к
нормальному при неограниченном росте числа
испытаний n. Теорема позволяет
вычислить вероятность попадания СВ в
интервал и вероятность отклонения по
абсолютной величине случайной величины от
своего математического ожидания:
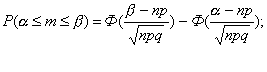
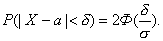
Пример1.
Диаметр детали, изготовленной цехом
является случайной величиной с дисперсией
0,0001 и математическим ожиданием 2,5 см. Найти
границы, в которых с вероятностью р=0,9973
заключен диаметр наудачу взятой детали.
Решение:
Используем
равенство
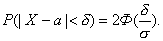
Данное
равенство можно использовать,
т.к. известно, что диаметр детали
распределен по нормальному закону.
Подставляя, получим:
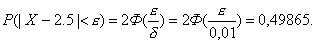
Откуда
Ф(t) = 0,9973, где t =
e/0,01
По
таблице находим t = e/0,01=
2,98, e
= 0,0298.
Тогда
диаметр детали заключен 2,5- 0,0298<x<2,5
+0,0298, т.е. 2,4702<x<2,5298.
Пример2.
Вероятность появления события А при каждом
испытании равна 0,7. Сколько раз нужно
провести испытание, чтобы с вероятностью 0,9
можно ожидать , что частота события А будет
отклоняться от вероятности не больше, чем
на 0,05?
Решение:
По
условию р= 0,7, тогда q
=0,3. Необходимо найти n.
Нужно,
чтобы условие |m/n-
0,7| <0,05 выполнялось с вероятностью 0,9.
Раскроем модуль и найдем границы для m:
0,65n< m < 0,75n. По
теореме Муавра - Лапласа:
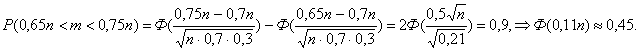
По
таблице находим
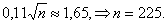

Контрольные
вопросы.
1.
В чем заключается суть закона больших
чисел?
2.
Сформулировать лемму Чебышева.
3.
Сформулировать терему Чебышева и ее
частный случай.
4.
Каким образом на практике применяется
теорема Чебышева?
5.
Сформулировать теорему Бернулли .
6.
Записать неравенство для оценки
вероятности отклонения частоты появления
события от ожидаемого результата.
7.
Между какими законами устанавливает
связь теорема Муавра- Лапласа?
Теоремы закона больших чисел
устанавливают зависимость между
случайностью и необходимостью.