ЛЕКЦИЯ 16

ТЕМА:  ЛИНЕЙНАЯ КОРРЕЛЯЦИЯ.

2. Коэффициент корреляции.

4. Расчет прямых регрессии по выборочным данным.

1.      Корреляционная зависимость.

Условимся обозначать через Х независимую переменную. а через У—зависимую переменную.

Зависимость величины Y от Х называется функциональной. если каждому значению величины Х соответствует единственное значение величины У.

 Обратим внимание на то, что если Х—детерминированная величина (т. е. принимающая вполне определенные значения), то и функционально зависящая от нее величина У тоже является детерминированной; если же X— случайная величина, то и У также случайная величина.

Однако гораздо чаще в окружающем нас мире имеет место не функциональная, а

стохастическая, или вероятностная, зависимость, когда каждому фиксированному значению независимой переменной Х соответствует не одно, а множество значений переменной У, причем сказать заранее, какое именно значение примет величина У, нельзя.

 Более частое появление такой зависимости объясняется действием на результирующую переменную не только контролируемого или контролируемых факторов (в данном случае таким контролируемым фактором является переменная X), а и многочисленных неконтролируемых случайных факторов. В этой ситуации переменная У является случайной величиной. Переменная же Х может быть как детерминированной, так и случайной величиной.

Если при изменении одной из величин изменяется среднее значение другой, то стохастическая зависимость называется корреляционной.

Приведем пример такой зависимости: пусть У – урожай зерна, Х – количество удобрений. С одинаковых по площади участков при равном количестве внесенных удобрений снимают разный урожай. Т.е. У не является функцией от Х. это объясняется влиянием случайных факторов: осадки, температура и т.п. Но опыт показывает что средний урожай является функцией от количества удобрений, У связан с Х корреляционной зависимостью: изменяя количество вносимых удобрений, изменяется и средний урожай, т.е. математическое ожидание величины У изменяется при изменении значения Х. Такое математическое ожидание называется условным и обозначается М( У/ Х= х) и читается: математическое ожидание СВУ при условии, что Х =х.

Тогда можно считать: корреляционная зависимость имеет место, если при изменении х изменяется условное математическое ожидание У.

Аналогично вводится понятие условного математического ожидания для СВХ.

g(x) =М(У/Х=х) и f(y) = М(Х/У=у) – называются функциями регрессии, а линию на плоскости, соответствующую этому уравнению – линией регрессии соответственно У на Х и Х на У. Эта линия показывает, как в среднем зависит У от Х или Х от У.

2.      Коэффициент корреляции.

Если Х и У являются независимыми случайными величинами, то М(ХУ) =М(Х)М(У). Если же Х и У зависимые, то М(ХУ) ¹ М(Х)М(У).

За меру зависимости Х и У принята безразмерная величина r, определяемая соотношением

r называется коэффициентом корреляции.

Случайные величины Х и У называются некоррелированными, если r =0, и коррелированными, если r¹ 0.

Пример1. Независимые СВ Х и У некоррелированные, т.к. r =0 (числитель равен нулю).

Пример2. Пусть между Х и У линейная зависимость, т.е. У = АХ +В.

Подставляя вместо У его выражение через Х и пользуясь свойствами математического ожидания получим r =1.

Свойства коэффициента корреляции:

1.      Если Х и У независимые СВ, то r =0;

2.      -1£ r £1 .При этом, если |r| =1, то между Х и У функциональная , а именно линейная зависимость;

3.      r характеризует относительную величину отклонения М(ХУ) от М(Х)М(У), и т.к. отклонение имеет место только для зависимых величин, то  r характеризует тесноту зависимости.

3.      Линейная корреляция.

Корреляционная зависимость между случайными величинами Х и У называется линейной корреляцией, если обе функции регрессии f(y) и g(x) являются линейными. В этом случае линии регрессии- прямые и называются прямыми регрессии.

Выведем уравнение прямой регрессии У на Х, т.е. найдем коэффициенты линейной функции   g(x) = AX +B.           

Введем обозначения  М(Х) =а, М(У) =b, D(X) =s₁², D(Y) ==s₂², М(ХУ) – М(Х)М(У) = m .

Используем свойства математического ожидания:

М(У) =М(g(x))= M(AX +B) = AM(X) +B, тогда B = b – Aa.

- называется коэффициентом регрессии У на Х. Уравнение прямой регрессии У на Х имеет вид :

Аналогично получим уравнение прямой регрессии Х на У :

Тогда уравнения примут вид:

Обе прямые проходят через общую точку (a; b) , угловые коэффициенты прямых регрессии равны:

 для прямой регрессии У на Х -

для прямой регрессии Х на У -

Чем ближе | r | к единице, тем меньше угол между прямыми регрессии, и только в случае | r | =1 прямые сливаются.

Коэффициент корреляции связан с коэффициентами регрессии соотношением:

4.      Расчет прямых регрессии по выборочным данным.

Пусть проведено n опытов, в результате которых получены следующие значения системы величин   (Х, У): (x_i ,y_i ), где i =1, 2, 3,…,n .

Математические ожидания и дисперсии Х и У заменим их точечными оценками: средними выборочными и выборочными дисперсиями:

Подставляя точечные оценки и приближенное значение r получим выборочные уравнения прямых регрессии:                                                                У на Х:

                                                         Х на У:

Пример: По выборочным данным, приведенным в таблице, найти выборочные уравнения прямых регрессии У на Х и Х на У, определить тесноту корреляционной зависимости.

Для удобства вычислений дополним таблицу:

Получим:

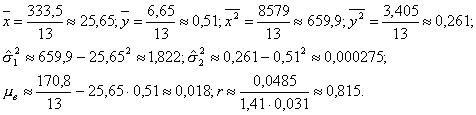
Уравнение прямой регрессии У на Х:

или             у = 0,01х + 0,255.

Уравнение прямой регрессии Х на У:

или                     х = 68,7у – 9,4.

Построим в одной системе координат данные точки и прямые регрессии:

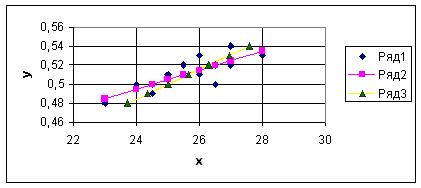
Ряд 1- данные точки, ряд 2- прямая регрессии У на Х, ряд 3 – прямая регрессии Х на У.

Коэффициент корреляции не равен нулю, значит присутствует зависимость величин Х и У; а т.к. r близок к единице, то можно предположить  наличие линейной зависимости. Предположение подтверждается расположением данных точек и полученных прямых регрессии: угол между прямыми регрессии мал и точки расположены близко к прямым регрессии.

Контрольные вопросы

1.      Какую зависимость называют стохастической?

2.      В каком случае стохастическая зависимость является корреляционной?

3.      Что такое функция регрессии?

4.      Сформулировать определение коэффициента корреляции и перечислить его свойства.

5.      В каком случае корреляционная зависимость является линейной корреляцией?

6.      Как производится расчет прямых регрессии по выборочным данным?