ЛЕКЦИЯ 8

ТЕМА: НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА

1.      Плотность распределения вероятностей. Интегральная функция распределения непрерывной случайной величины.

2.      Числовые характеристики непрерывной случайной величины.

1. Плотность распределения вероятностей. Интегральная функция распределения НСВХ.

Напомним определение непрерывной случайной величины:

Непрерывной случайной величиной (НСВ) называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Множество возможных значений непрерывной случайной величины бесконечно и несчетно.

 Диаметр изготавливаемой детали на станке- непрерывная случайная величина, т.к. возможны отклонения из-за возникающих погрешностей ввиду температурных изменений, силы трения, неоднородности материала и т.д., а диаметр может принять любое значение из промежутка (c, d).

Непрерывную случайную величину, так же как и ДСВ, можно задать с помощью функции распределения, которая равна вероятности того, что СВХ приняла значение меньшее заданного х. Для вывода формулы функции распределения НСВХ познакомимся сначала с плотностью распределения вероятностей НСВХ.

Введем ограничение: рассмотрим только такие СВХ, для которых вероятность попадания в интервал                    (х; х+Dх) , где Dх>0 и Dх®0, пропорциональна длине интервала Dх, т.е.Р(х, х+Dх)» р(х)Dх, где р(х)- коэффициент пропорциональности, р(х) Dх- элемент вероятности. Выясним его смысл с помощью полученного приближенного равенства:  

Следовательно, р(х)- есть вероятность , которая приходится на единицу длины , рассматриваемого участка и равна производной интегральной функции распределения. Поэтому р(х) называют плотностью распределения вероятностей или дифференциальной функцией распределения.

Если все значения НСВХ принадлежат некоторому интервалу (а; в), то интегральная функция распределения имеет вид :

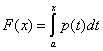
Если НСВХ может принять любое действительное значение, то функция имеет вид:

Вероятность попадания НСВХ в некоторый интервал (a,b) равна :

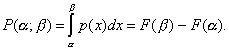
Из геометрического смысла определенного интеграла следует, что вероятность попадания НСВХ в заданный интервал равна площади криволинейной трапеции, ограниченной осью абсцисс, прямыми х = а и х= b графиком функции р(х), который называется кривой распределения вероятностей.  

Т.к. в результате опыта случайная величина обязательно примет какое -либо из возможных значений, то :

или

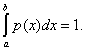
2.      Числовые характеристики непрерывной случайной величины.

При введении понятия математического ожидания   воспользуемся понятием элемента вероятности

р(х) Dх.

Предположим, что все возможные значения случайной величины Х принадлежат отрезку [а, b]. Разобьем произвольным образом этот отрезок точками а=x₀<x₁<x₂<…<x_n=b на п частичных отрезков. В каждом таком частичном отрезке, длина которого D х,, произвольно возьмем точку h_i, где i=l, 2, 3, ..., п.  Известно, что вероятность попадания значения непрерывной случайной величины на отрезок Dх приближенно равна р(х)Dx (элемент вероятности) и поэтому приближенно будем считать, что случайная величина Х может принять n значений h_i на отрезке [а, b] с вероятностями р(h_i) Dx_i. Теперь можно воспользоваться формулой, задающей математическое ожидание для дискретной случайной величины. В результате будем иметь

 Переходя к пределу в правой части равенства, имеем:

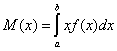
Если возможные значения случайной величины распределены по всей оси Ох, то

Здесь предполагается, что несобственный интеграл сходится абсолютно, т. е. существует.

Т.к. дисперсия случайной величины есть математическое ожидание квадрата отклонения случайной величины от своего математического ожидания, то

Дисперсией непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называется определенный интеграл

  или

  .

При вычислении дисперсии НСВХ также можно пользоваться формулой

Свойства математического ожидания и дисперсии НСВХ аналогичны свойствам числовых характеристик ДСВХ.

Рассмотрим примеры решения задач.

Пример 1. НСВХ задана интегральной функцией

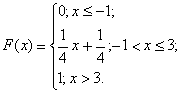
Найти вероятность того, что НСВХ примет значение из интервала(-2;2).

Решение:

Пример 2. НСВХ задана плотностью распределения

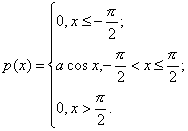
Найти вероятность попадания в интервал (-p;p/4).

Решение: Найдем коэффициент а из условия

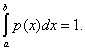
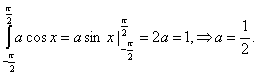
Все значения НСВХ распределены на интервале (-p/2; p/2),тогда задача сводится к вычислению вероятности попадания НСВХ в интервал (-p/2; p/4):

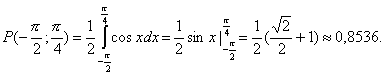
3. Задан график интегральной функции распределения НСВХ (парабола с вершиной в начале координат). Задать НСВХ аналитически. Найти плотность распределения р(х) и построить ее график, вероятность попадания в интервал (-2;4), числовые характеристики.

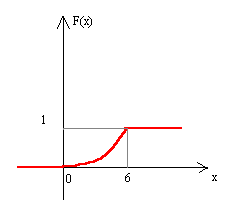
Решение: Все значения НСВХ распределены на интервале (0;6). И данном интервале графиком функции F(x) является парабола, уравнение которой y= k x². Найдем k, подставив в уравнение параболы координаты точки (6;1):

1=36 k, откуда k= 1/36.  Тогда интегральная функция имеет вид:

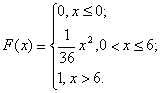
Плотность распределения равна первой производной интегральной функции:

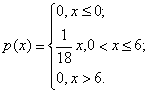
Построим ее график:

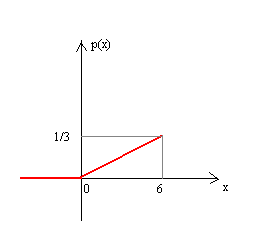
Вычислим вероятность попадания НСВХ в интервал (-2;4). Т.к. левее х=0 вероятность равна нулю, вычислим вероятность попадания в интервал (0;4):

Найдем числовые характеристики:

Контрольные вопросы

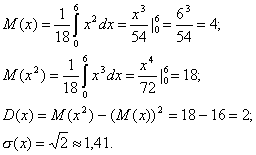
1.        Сформулировать определение непрерывной случайной величины.

2.        Что такое плотность распределения вероятностей?

3.        Каким свойством обладает плотность распределения вероятностей?

4.        Как найти интегральную функцию, зная плотность распределения и наоборот?

5.        Перечислить свойства интегральной функции.

6.        Дать определения числовым характеристикам НСВХ.